Derivative of the Tangent Squared Function In this tutorial we shall discuss the derivative of the tangent squared function and its related examples It can be proved by the definition of differentiation We have a function of the form y = f ( x) = tan 2 x By the definition of differentiation we have d y d x = lim Δ x → 0Derivative tan^2x מחשבון נגזרת Symbolab נגזרות נגזרת ראשונה נגזרת שנייה נגזרת שלישית נגזרת מסדר גבוה נגזרת בנקודה נגזרת חלקית נגזרת של פונקציה סתומה That is, the derivative of the function ƒ(x) = e 2x is ƒ'(x) = 2e 2x This derivative tells us the rate of change the output of the original function per change in input Basically, the two equations tell us that the output of the function ƒ(x) = e 2x grows by a factor of 2e 2x per input So if our x value is one, plugging that value into
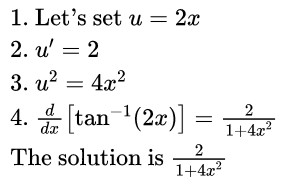
Derivative Of Arctan X Inverse Tangent Detailed Lesson
Derivative of tan 2x
Derivative of tan 2x-Given a function , there are many ways to denote the derivative of with respect to The most common ways are and When a derivative is taken times, the notation or is used These are called higherorder derivatives Note for secondorder derivatives, the notation is often used At a point , the derivative is defined to be The derivative of sec x tan x In simple language, keep the initial term as it is and distinguish the second term, then distinguish the first term and keep the next term since it is or viceversa What is the derivative of SEC 2x?



Differentiate The Following From First Principles I Tan 2 X Ii Tan 2x 1 Sarthaks Econnect Largest Online Education Community
Example 16 Calculate the derivative of the function \y = \left( {2 {x^2}} \right)\cos x 2x\sin x\ at \(x = \pi\)Find dy/dx tan(2xy)=2x Differentiate both sides of the equation Differentiate the left side of the equation By the Sum Rule, the derivative of with respect to is Since is constant with respect to , the derivative of with respect to is Differentiate using the Power Rule which states that is whereCreate your account View this answer The derivative of tan 1 is 2 14x2 2 1 4 x 2 Finding the derivative of this function will involve the
The derivative of sin x is cos x, The derivative of cos x is −sin x (note the negative sign!) and The derivative of tan x is sec 2x Now, if u = f(x) is a function of x, then by using the chain rule, we have d ( sin u) d x = cos u d u d xThe slope of a line like 2x is 2, or 3x is 3 etc;Piece of cake Unlock StepbyStep derivative of tan^2x Natural Language Math Input NEW Use textbook math notation to
Differentiate the following from first principle tan 2x > 11th > Maths > Limits and Derivatives > Derivative of Trigonometric Functions > Differentiate the followingLet's first think about a function of one variable (x) f(x) = x 2 We can find its derivative using the Power Rule f'(x) = 2x But what about a function of two variables (x and y) f(x, y) = x 2 y 3 We can find its partial derivative with respect to x when we treat y as a constant (imagine y is a number like 7 or something) f' x = 2x 0 = 2xThe derivative of tan 2x is 2 sec 2 (2x) (ie) d/dx tan 2x = 2 sec 2 (2x) Explanation We know that the derivative of tan x is sec 2 x (ie) d/dx (tan x) = sec 2 x According to the chain rule,




Differentiate The Following From First Principle Tan2x Youtube




Ex 13 1 22 Lim X Pi 2 Tan 2x X Pi 2 Chapter 13 Class 11
Solution We know that tan x can be expressed in terms of sin and cos tan x = sin / cos x Hence tan2x = sin2x/cos2x tan 2 x = sin 2 x / cos 2Answer (1 of 3) Oh dear goodness, this is going to be such a nightmare I suppose it's allowed as "first principles" to use the definition of derivative \displaystyle \frac{d}{dx} \tan(x^2) = \lim_{h \to 0} \frac{\tan((xh)^2)\tan(x^2)}{h} Hopefully it's also allowed as "first principles"Figure 1 Graphs of 2tan2 x (blue) and sec x (red) In fact, that is the case sin2 x tan2 x = cos2 x 1 2− cos x = cos2 x = sec 2 x − 1 1 2 1 2 1 We conclude that tan x = sec and so the two results are equiva 2 2 x − 2 lent up to an added constant Both answers are correct 2




Differentiation Of Tan 2 X And X 3 X 4 Youtube




Brandi S Buzzar Blog Proof Derivative Tan X Sec 2 X
Derivative of 3(tan(2x))^2 Simple step by step solution, to learn Simple, and easy to understand, so don`t hesitate to use it as a solution of your homework Below you can find the full step by step solution for you problem We hope it will be very helpful for you and it will help you to understand the solving processThe Derivative tells us the slope of a function at any point There are rules we can follow to find many derivatives For example The slope of a constant value (like 3) is always 0; The second derivative of tan^2x is 4sec 2 (x)tan 2 (x) 2sec 4 (x) Interesting property of the derivative of tan^2x It is interesting to note that the derivative of tan 2 x is equal to the derivative of sec 2 x



Find The Derivative Of Arctan Tan2 X Stumbling Robot
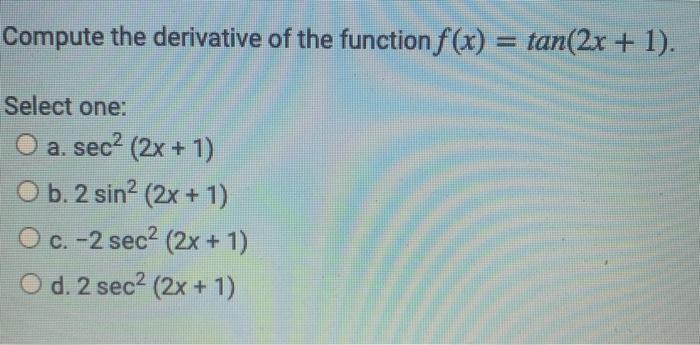



Solved Compute The Derivative Of The Function F X Tan 2x Chegg Com
About Press Copyright Contact us Creators Advertise Developers Terms Privacy Policy & Safety How works Test new features Press Copyright Contact us CreatorsDerivative of tan(2x)^3 Simple step by step solution, to learn Simple, and easy to understand, so don`t hesitate to use it as a solution of your homework Below you can find the full step by step solution for you problem We hope it will be very helpful for you and it will help you to understand the solving processTranscribed Image Text Find the derivative of the function y = 6 In sin 22x O A 24 sin 2x OB 12 In sin 2x C 24 cot 2x O D 4 tan 2x check_circle




The Derivative Of Tan 2x Derivativeit




bestpictjcry Tan 2x Tan 2x
Derivative of \(tanx = sec^2x \) What Is The Derivative Of tan(x)?Derivatives of Tangent, Cotangent, Secant, and Cosecant We can get the derivatives of the other four trig functions by applying the quotient rule to sine and cosine For instance, d d x ( tan {eq}\displaystyle \sec^{2}(x) {/eq} is the derivative of tan(x) for x One can find the derivative of tan(x) using the definition of tan(x) in terms of



The Derivative Of Tan X Is 1 Cos X 2 Use The Chain Rule To Find Tan X 2




Larson Calculus 5 4 52 Find The Derivative Of Y E 2x Tan 2x With The Product Rule Youtube
The inverse tangent — known as arctangent or shorthand as arctan, is usually notated as tan1 (some function) To differentiate it quickly, we have two options 1) Use the simple derivative rule 2) Derive the derivative rule, and then apply the rule In this lesson, we show the derivative rule for tan1 (u) and tan1 (x) There are four The derivative of the former is $\frac{1}{1x^2}$, and the derivative of $\tan(x)$ is $\sec^2(x)$ Share Cite Follow answered Mar 25 '19 at 2147 Dave Dave 126k 1 1 gold badge 16 16 silver badges 37 37 bronze badges $\endgroup$ 3 Derivative of tan (2x) = 2sec 2 (2x) The Second Derivative Of tan(2x) To calculate the second derivative of a function, you just differentiate the first derivative




Find The Derivative Of The Given Function Y Tan 2x 1 Cot 2x I Tried Converting The Original Function In Terms Of Sin And Cos But It Was Still Too Complicated To Be Called Simplified




Derivative Of Tan X Sec X Tan X More
Free derivative calculator differentiate functions with all the steps Type in any function derivative to get the solution, steps and graphSolution for 5 Find the derivative of the following 3x5 а у3 b y = In (sin(3x5)) c y= e2x arc tan (2x 3) x1Partial derivative of tan (2xy) \square!




Solved Differentiate The Following Function With Respect To Chegg Com




The Derivative Of Tan X Is Sec 2 X Why Mathematics Stack Exchange
Answer (1 of 4) Let f(x)=\tan^3 (x) We can express f(x) as a composite function Let g(x)=x^3 and h(x)= \tan (x) f(x)=g(h(x)) Using the chain rule, we know that f'(xThe tangent line is the best linear approximation of the function near that input value For this reason, the derivative is often described as the "instantaneous rate of change", the ratio of the instantaneous change in the dependent variable to that of the independent variable The derivative of tan x The derivative of tan x is sec 2 x Show activity on this post The instructions Use the definition of derivative to find f ′ ( x) if f ( x) = tan 2 ( x) I've been working on this problem, trying every way I can think of At first I tried this method lim h → 0 tan 2 ( x h) − tan 2



Solved The Second Derivative Of Y Tan 2 X Is A Y 2 Chegg Com




What Is The Integration Of Tan 2x Solution Quora
The derivative of tan x with respect to x is denoted by d/dx (tan x) (or) (tan x)' and its value is equal to sec 2 x Tan x is differentiable in its domain To prove the differentiation of tan x to be sec 2 x, we use the existing trigonometric identities and existing rules of differentiation We can prove this in the following ways Proof by first principleDerivative of inverse tangent Calculation of Let f (x) = tan 1 x then,Get stepbystep solutions from expert tutors as fast as 1530 minutes Your first 5 questions are on us!




91 Derivative Of Tan 2x Youtube




Solved Q 4 Find The Derivative Of F X X Tan 2x Q 5 Find Chegg Com
The derivative of tan 2x can be calculated using different methods such as the chain rule and quotient rule Let us determine the derivative of tan 2x using the chain rule d(tan 2x)/dx = d(tan 2x)/d(2x) × d(2x)/dx = sec 2 2x × 2 = 2 sec 2 (2x) Hence the derivative of tan 2x is 2 sec 2 (2x) Now, we will determine the integral of tan 2x Example 22 Find the derivative of tan (2x 3) Let y = tan (2x 3) We need to find derivative of y, ie 𝑑𝑦/𝑑𝑥 = (𝑑 tan〖(2𝑥3)〗)/𝑑𝑥Become a Studycom member to unlock this answer!




Derivative Rules For Trigonometric Functions



Leslie Ruo S Blog Rusty Calculus
The derivative of `f(x)=tan(2x pi/2)` is `f'(x) = 2*sec^2(2x pi/2)` and at `x = 3*pi/4` the slope of the tangent is 2 Approved by eNotes Editorial Team Luca BGraph of tan x and its Derivative The graphs of \( \tan(x) \) and its derivative are shown below Derivative of the Composite Function tan (u(x)) We now have a composite function which is a function (tan) of another function (u)Derivative Calculator computes derivatives of a function with respect to given variable using analytical differentiation and displays a stepbystep solution It allows to draw graphs of the function and its derivatives Calculator supports derivatives up to




How To Differentiate A Function Of Tan Tanf X Derivative Of Tan 2x Tan X 2 Tan X Youtube




Ii 1 Find The Derivatives Of The Following Functions From The First Principles X3 I X4 4 Iii Ax Bx C Iv Vx 1 V Sin 2x Vi Cos
The basic trigonometric functions include the following \(6\) functions sine \(\left(\sin x\right),\) cosine \(\left(\cos x\right),\) tangent \(\left(\tan x\rightThe derivative of sec2 (x) is 2sectwo (x) tan (x) The chain rule says the derivative of f (g (x)) is equivalent toEg1 Write sinxcosxtanx as sin(x)cos(x)tan(x) 2 Write secx*tanx as sec(x)*tan(x) 3 Write tanx/sinx as tan(x)/sin(x) 4 Use inv to specify inverse and ln to specify natural log respectively Eg1 Write sin1 x as asin(x) 2 Write ln x as ln(x) 5 Sample Inputs for Practice Eg1 Write (10x2)(x 2) as 10*x2x^2 2 Write cos(x 3) as cos




Differentiation Of Tanx 2 Youtube




Solved Question 4 Find The Derivative Of F X 2x Sec2x O Chegg Com
About Press Copyright Contact us Creators Advertise Developers Terms Privacy Policy & Safety How works Test new features Press Copyright Contact us Creators\( \frac{d}{dx} {tanx} = \frac{d}{dx} \frac{sinx}{cosx}\) we know that \( tanx =\frac{sinx}{cosxTo apply the Chain Rule, set u u as tan ( x) tan ( x) Differentiate using the Power Rule which states that d d u u n d d u u n is n u n − 1 n u n 1 where n = 3 n = 3 Replace all occurrences of u u with tan ( x) tan ( x) The derivative of tan(x) tan ( x) with respect to x x is sec2(x) sec 2 ( x) Reorder the factors of 3tan2(x)sec2




Solved Find The Derivative 29 Y 8 10 Secx A Y 10 Chegg Com
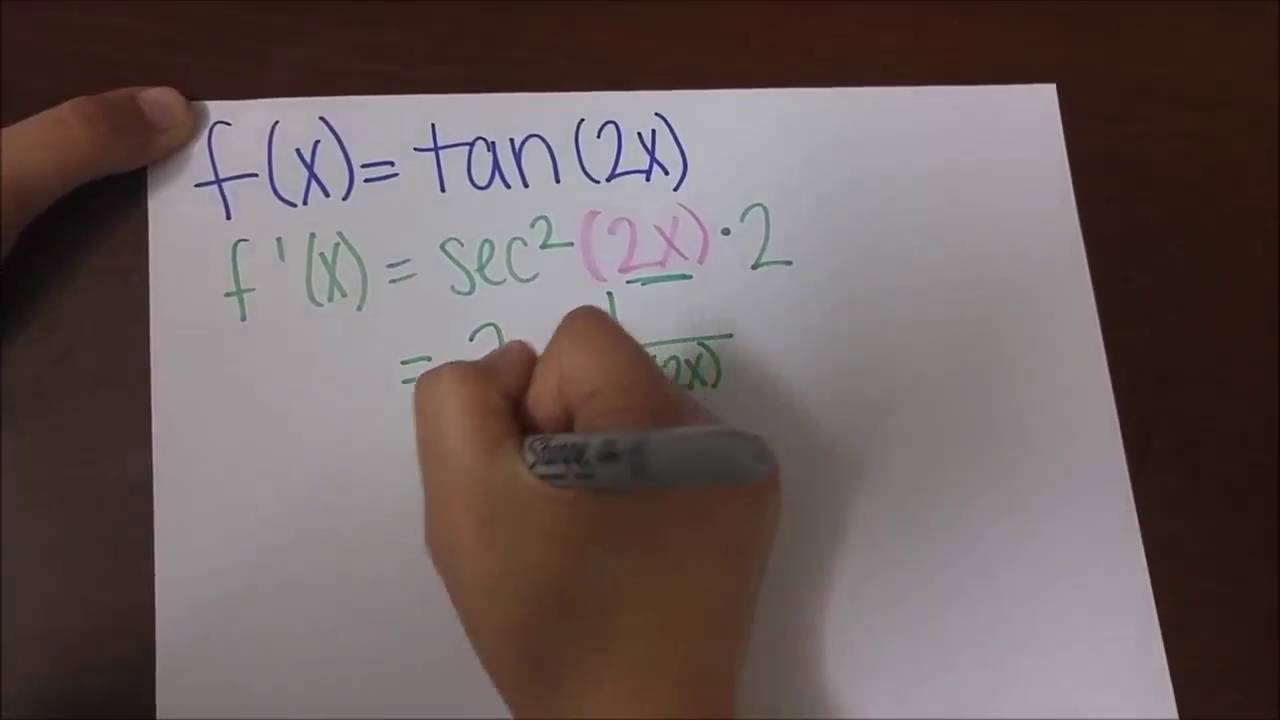



Ii F Find Derivative Of Tan 2x At X Pi 6 Youtube
Derivative of tan^2x WolframAlpha Volume of a cylinder?An older video where Sal finds the derivative of tan (x) using the quotient rule Created by Sal Khan Trigonometric functions differentiation Derivatives of tan (x) and cot (x) Derivatives of sec (x) and csc (x) Practice Derivatives of tan (x), cot (x), sec (x), and csc (x) Worked example Derivative of sec (3π/2x) using the chain rule Derivative of tan^2 x We have the derivative of tan square x So, let y be equal to tan square x Differentiate with respect to x, dy upon dx equals the derivative of tan square x Now it will be tan x whole square upon d tan x into d tan x upon dx After we apply the xn formula, it will be two tan x times sec squared x




Lesson 3 5 Chain Rule Or Usubstitutions Objectives




Question Video Differentiating Trigonometric Functions Nagwa
And so on Here are useful rules to help you work out the derivatives of many functions (with examples below)Note the little mark ' means derivative of, and



How Do I Integrate Tan 2 X Youtube




Finding The Derivative Of Sec 2 X Video Lesson Transcript Study Com



Derivative Of Tan2x Sin2x Cos2x And 2tanx 1 Tan 2x Youtube



What Is The Formula Of Tan2x Quora




If Y Tanx Tan2x Tan3x Then Dy Dx




Solved 6 Find The Derivative Of The Following Functions Do Chegg Com
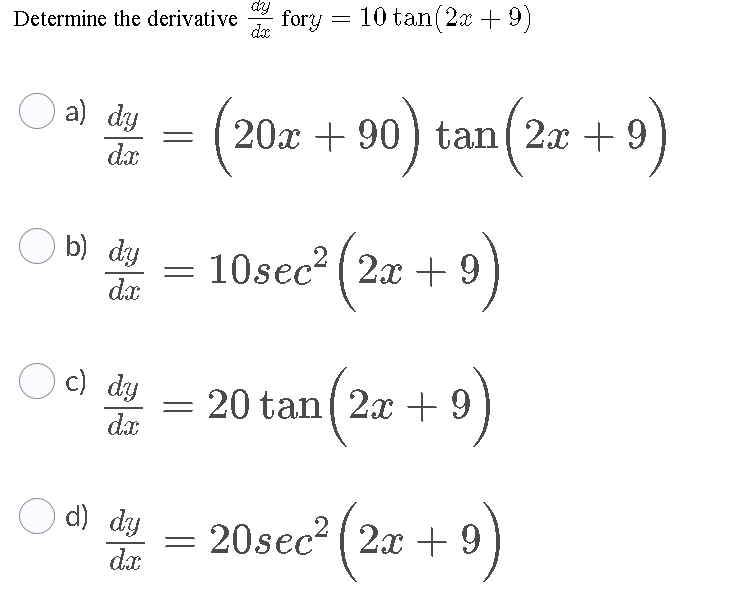



Solved Determine The Derivative Fory 10 Tan 2x 9 O A Dy Chegg Com




Finding The Derivative Of Sec 2 X Video Lesson Transcript Study Com




06 Derivative By Substitution Of Trigonometric Ratio Tan 2 X 3 2tans Tan2x Youtube
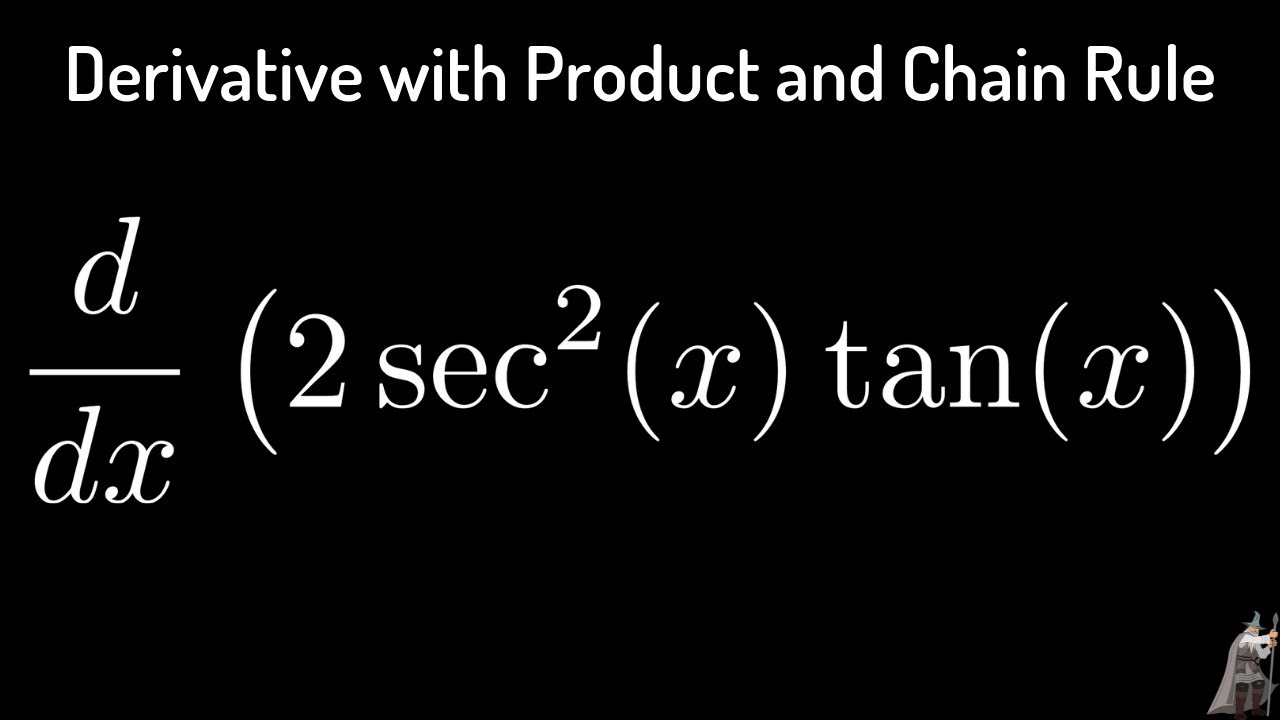



The Derivative Of H X 2 Sec 2 X Tan X Product Rule Example Youtube




Solved The Second Derivative Of Y Tan 2x Is A Y 4 Secº Chegg Com



1
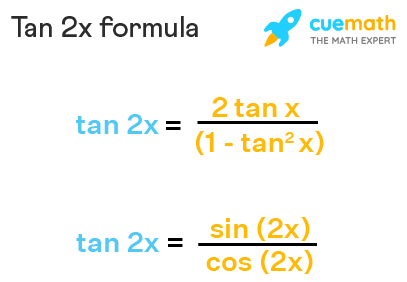



Tan 2x Formula What Is Tan 2x Formula Examples




Solved The Second Derivative Of Y Tan 2 X Is A Y 2 Chegg Com
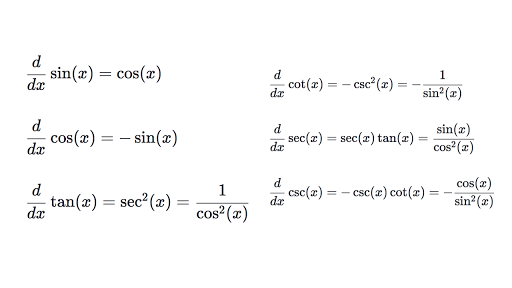



Differentiating Trigonometric Functions Review Article Khan Academy



Differentiate The Following From First Principles I Tan 2 X Ii Tan 2x 1 Sarthaks Econnect Largest Online Education Community



1
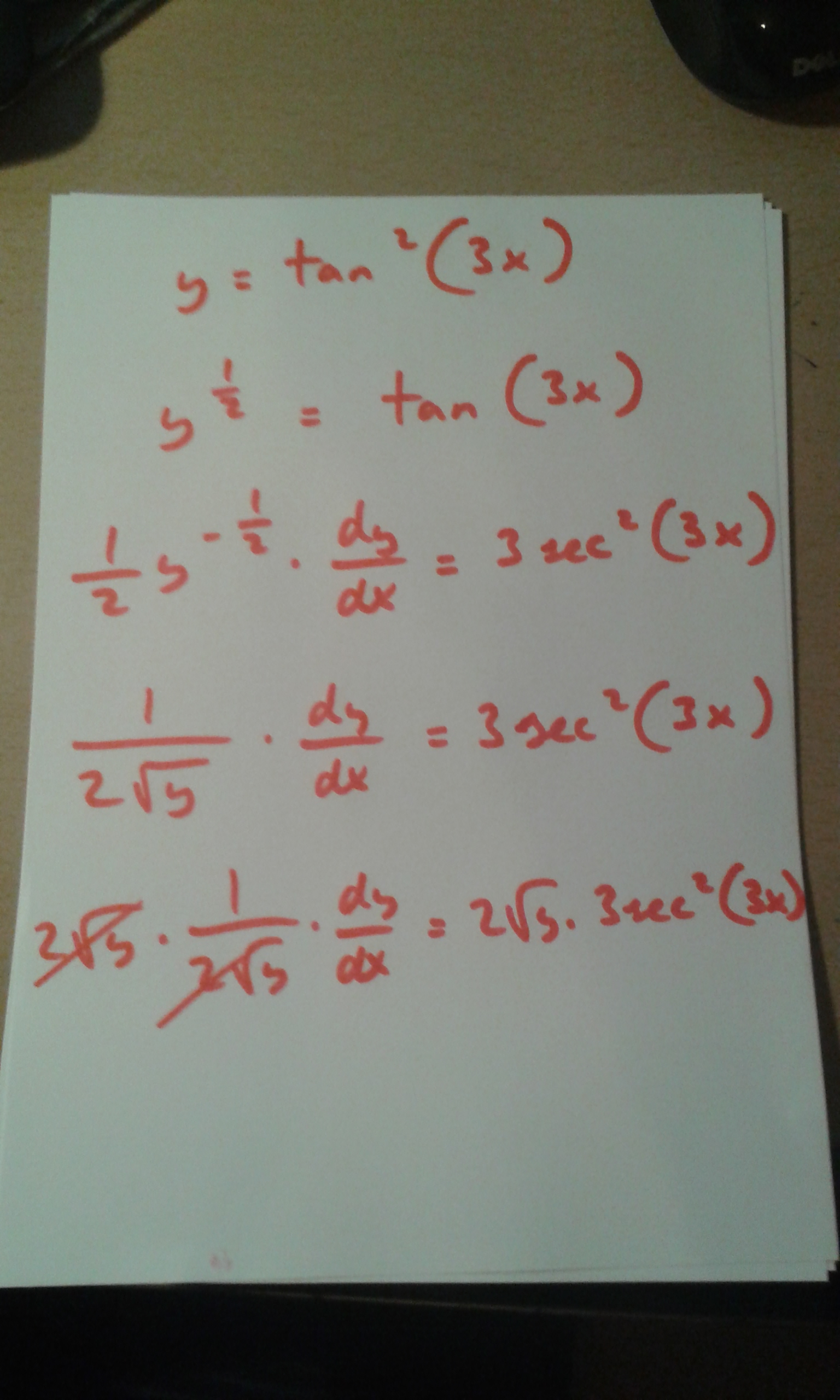



How Do You Find The Derivative Of Tan 2 3x Socratic




Tan2 Derivative ただの悪魔の画像




How To Find Second Derivative Of F X Ln Tanx Calculus



What Is The Differentiation Of Sec Inverse Tan 2x Quora
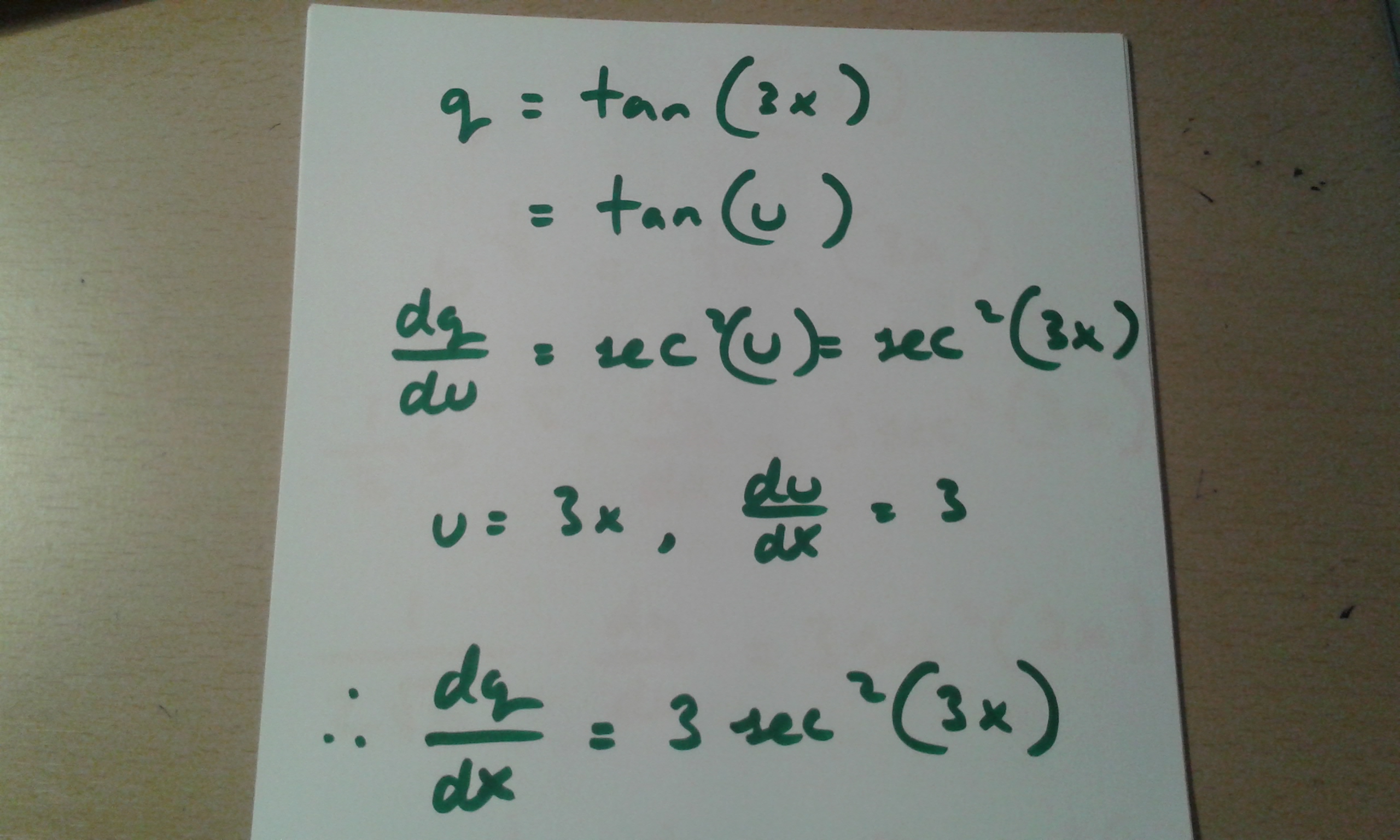



How Do You Find The Derivative Of Tan 2 3x Socratic




Chapter 3 Differentiation 1 3 1 The Derivative
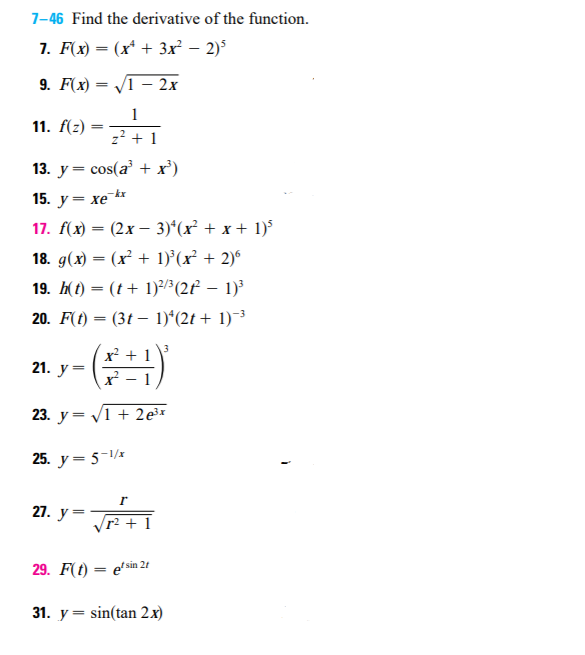



Solved 7 46 Find The Derivative Of The Function 13 Chegg Com




How To Take The Derivative Of Tan X Video Lesson Transcript Study Com
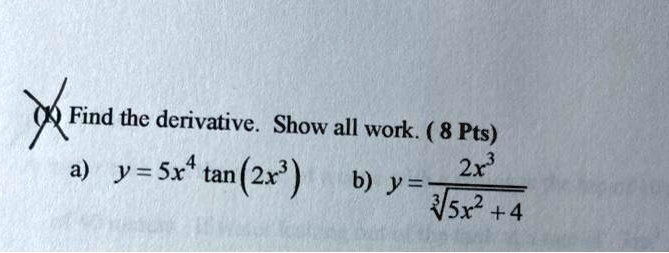



Mm8f Uuc1yooam



What Is The Nth Derivative Of Tan 1 2x 1 X 2 Quora
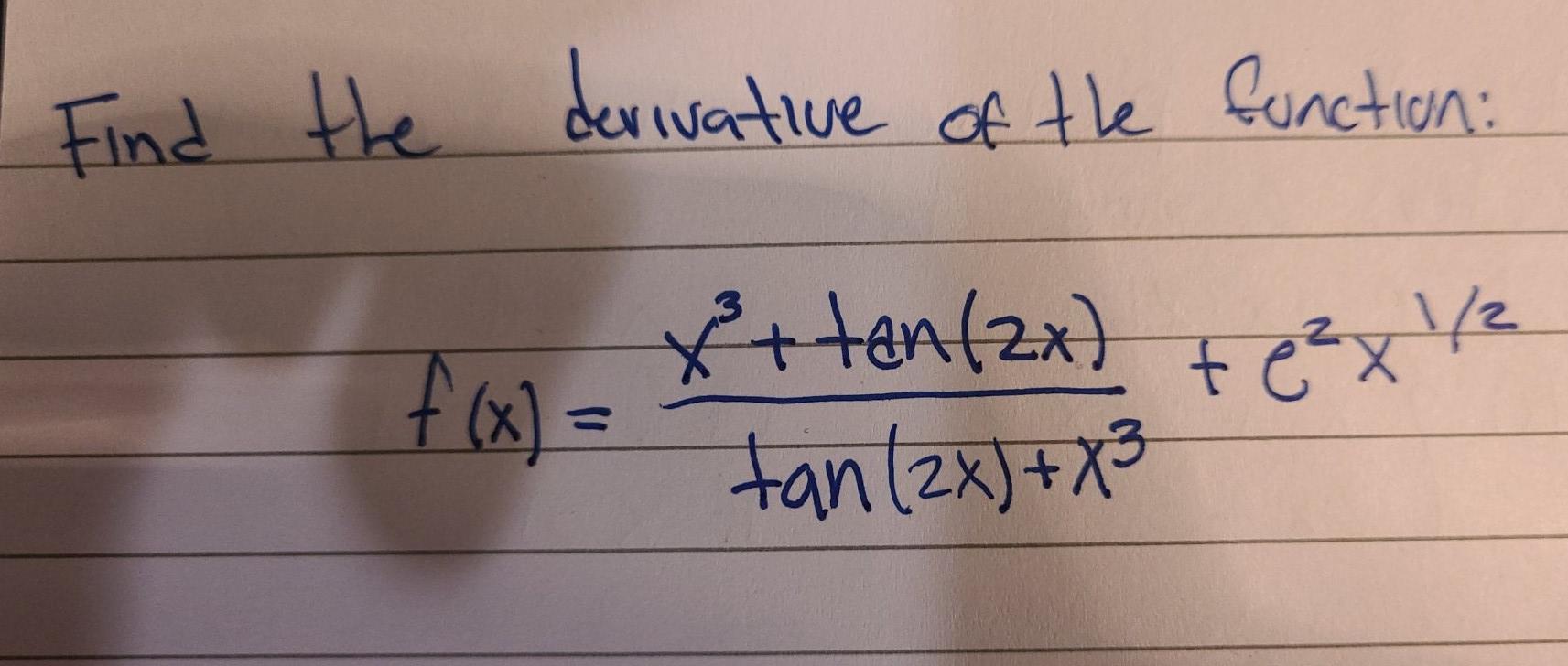



Solved Find The Derivative Of The Function X Tan 2x X Chegg Com
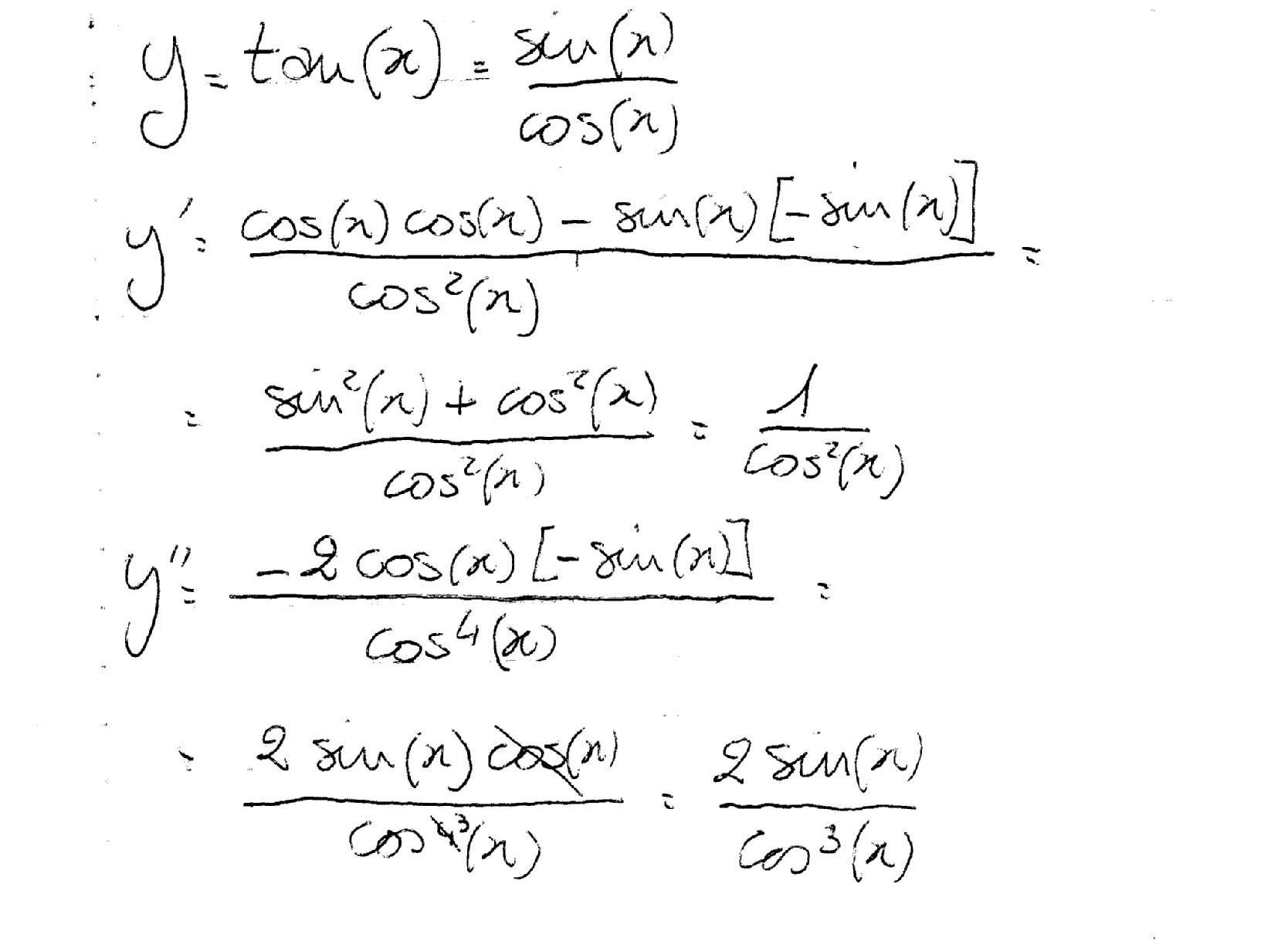



What Is The 2nd Derivative Of Y Tanx Socratic




Solved 1 Differentiate The Following With Respect To X Y Chegg Com




Solved 4 2rv Nte Ja Aiv Frr Am Br A Bh Tor Vny Trr T Ixr Ans V Tr 6 T X A8 Hint A A Ans I2a X Ay 3bx Ons Yt




Solved The Second Derivative Of Y Tan 2 X Is A Y 2 Chegg Com
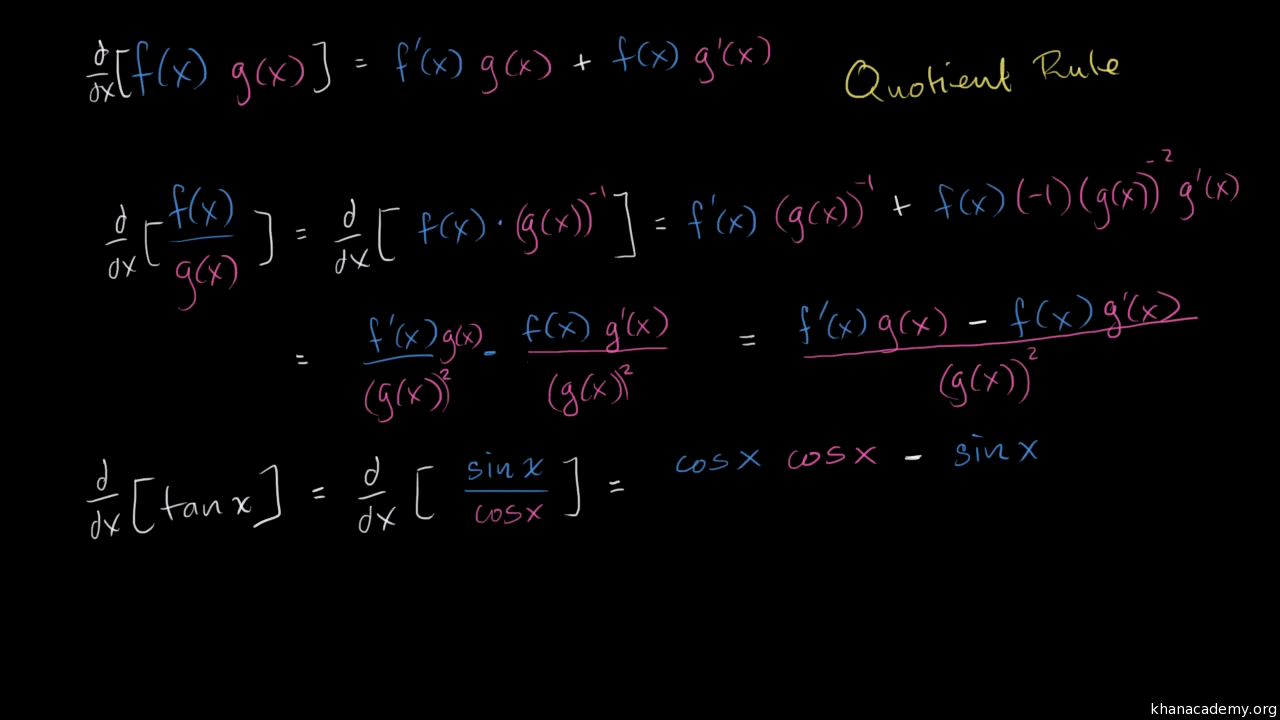



Derivative Of Tan X Old Video Khan Academy




Solved 7 Find The Derivative Of The Function 16 Y 11 Chegg Com




Maclaurin Series Tan X
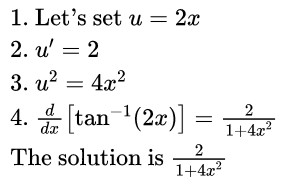



Derivative Of Arctan X Inverse Tangent Detailed Lesson



Find The Derivative Of The Function Tan 2x 3 From The Definition First Principles Sarthaks Econnect Largest Online Education Community




Differentiate Tanx Tan 2x Tan 3x Tan 4x W R T X Youtube
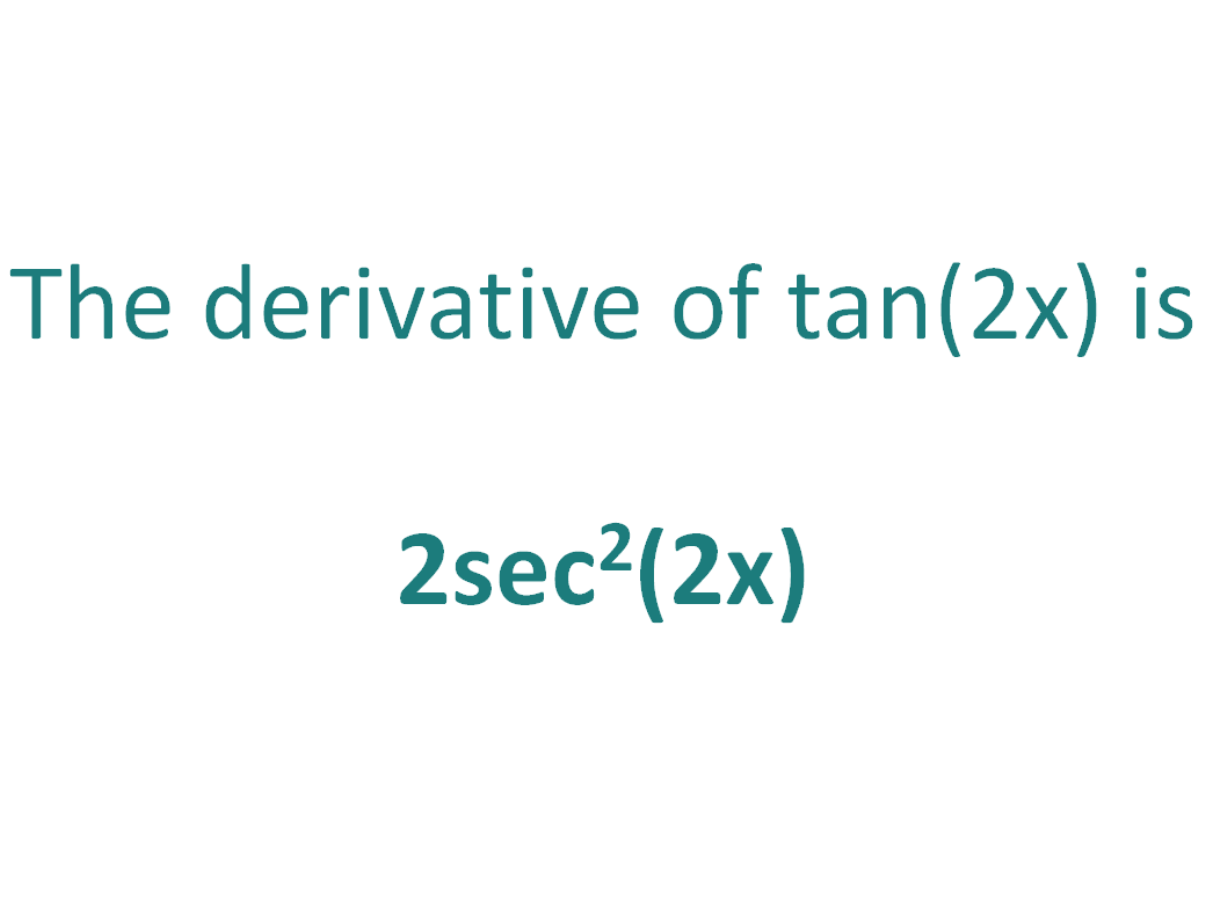



The Derivative Of Tan 2x Derivativeit




Derivative Of Tangent Slope Derivative More




Solved Which Of The Following Is The Derivative Of x Chegg Com




Prove That Derivative Of Tan X Is Sec 2 X By First Principle




Derivative Of Tan 2x 3 From First Principle Brainly In



1
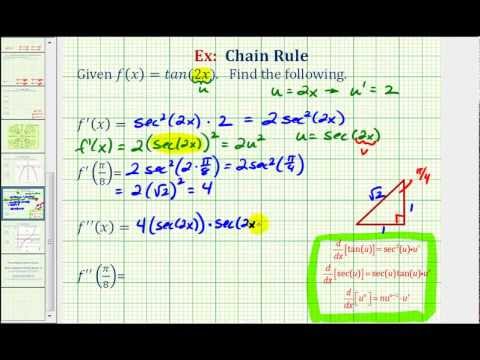



Ex 1 First And Second Derivatives Using The Chain Rule F X Tan 2x Youtube




Ap Calculus Ab How Do I Find The Derivative Of The Trig Function Of A Trig Function Y Sin Tan2x Homeworkhelp




Derivative Of Tangent X Sec X Tan X Longer Free Tutorial Get Education Bee




Example 22 Find Derivative Of Tan 2x 3 Chapter 5 Class 12



What Is The Derivative Of Tan 1 Sec X Tan X Quora




Derivatives Of Trigonometric Functions




Differentiate The Following From First Principle Tan 2x



Solved Let F X Tan 2x Tanx Determine The Local Extrema Intervals Of Increasing And Decreasing Of F X Course Hero
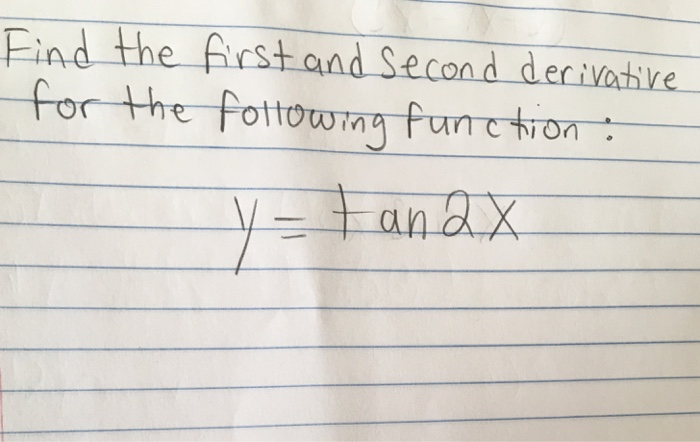



Solved Find The First And Second Derivative For The Chegg Com




Prove That Derivative Of Tan X Is Sec 2 X By First Principle




Proof That The Derivative Of Tan X Sec 2x Using The Quotient Rule Album On Imgur
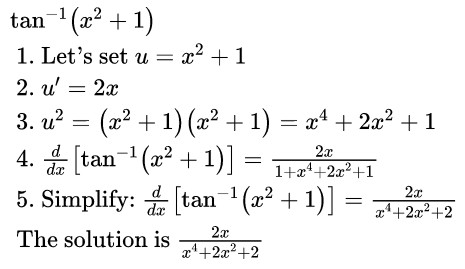



Derivative Of Arctan X Inverse Tangent Detailed Lesson




Derivative Of Tan 2x 3 Is A 2sec 2x 3 B Sec 2x 3 C Sec 2x 3 D None Of These Snapsolve
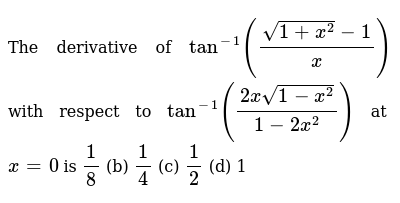



The Derivative Of Tan 1 Sqrt 1 X 2 1 X With Respect To Tan 1 2xsqrt 1 X 2 1 2x 2 At X 0 Is 1 8 B 1 4 C 1 2 D 1



Derivative Of Inverse Tangent




Differentiation With Trig Outcomes Ppt Download




Tan 2x Formula What Is Tan 2x Formula Examples
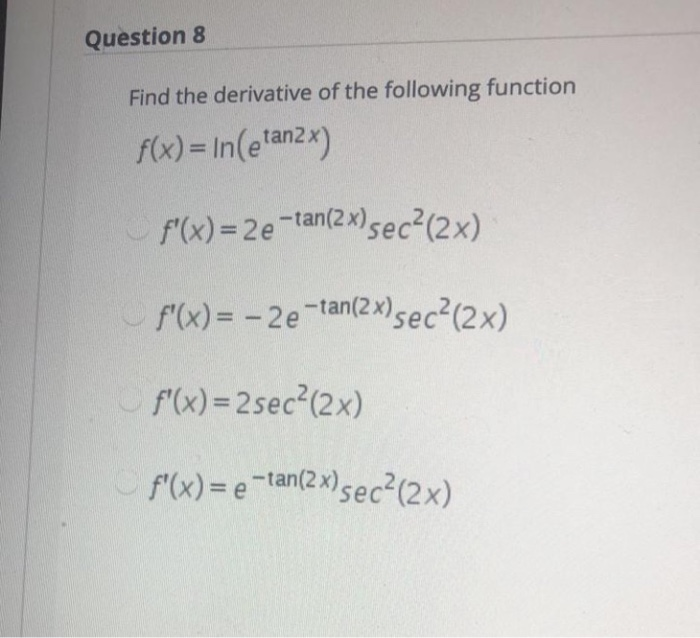



Solved Question 7 Find The Derivative Of The Following Chegg Com




The Derivative Of Tan 2x W R T Cos 2x Is Maths Limits And Derivatives Meritnation Com




Pvkcw6ipjmk Xm
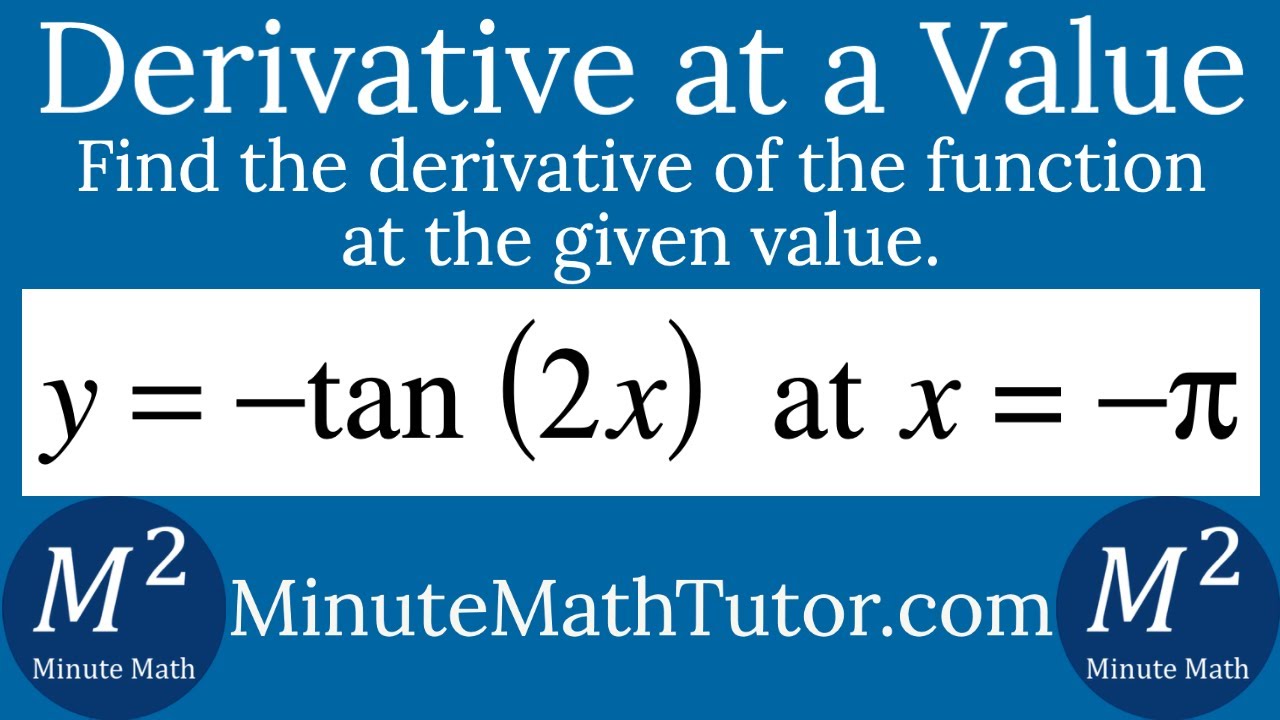



Find The Derivative Of Y Tan 2x At X P Youtube



1



What Is Integral Of Sin2x Tan2x Quora




Solved Question 1 Integrate The Following Function Sec 2x Chegg Com




Prove That Derivative Of Tan X Is Sec 2 X By First Principle




Solved A Differentiate The Following Function With Respect Chegg Com




Differentiate The Following From First Principle Tan 2x 1



Derivative Of Tangent X Sec X Tan X Longer Free Tutorial Get Education Bee




Find The Derivative Of Tan 2x 3 Youtube




Second Derivative Of Tan 2x Youtube




Integration Of Inverse Tan 2x Integration By Parts Youtube




05 Derivative Of Tangent Function Tan2x And Tanx 2 Youtube



0 件のコメント:
コメントを投稿